🎯 Writing a Semantle Solver

Last year, I stumbled upon this 3Blue1Brown video (and its follow-up) about the game Wordle. The narrator explains how to find the optimal first guess using information theory. At the time, I had discovered another word guessing game called Semantle; unlike Wordle, which gives hints based on what letters the guesses share with the target word, Semantle gives hints based on how similar in meaning the guesses are to the target word.

Naturally, we might wonder: “is there an optimal first word to guess in Semantle to minimize the number of guesses?” — or perhaps more generally, “is there an optimal strategy for minimizing the number of guesses?”

A Semantle game in action — more details about the gameplay below!

Semantle Mechanics

The rules of Semantle are as follows:

Each game chooses a random word to be the target.
We can repeatedly make a guess, which is a word or sometimes a multi-word term
After each guess, the game outputs a similarity score, which represents how close the guess is to the target. If our guess is in the closest 1000 words to the target, then the game will tell us what rank that guess is, called the proximity.

When the similarity score is high, it can help dictate our next guess; however, most guesses don’t guide us much. When the similarity score is below 25 and we haven’t guessed any of the closest 1000 words, we still often need to stumble around to make more progress!^[1]

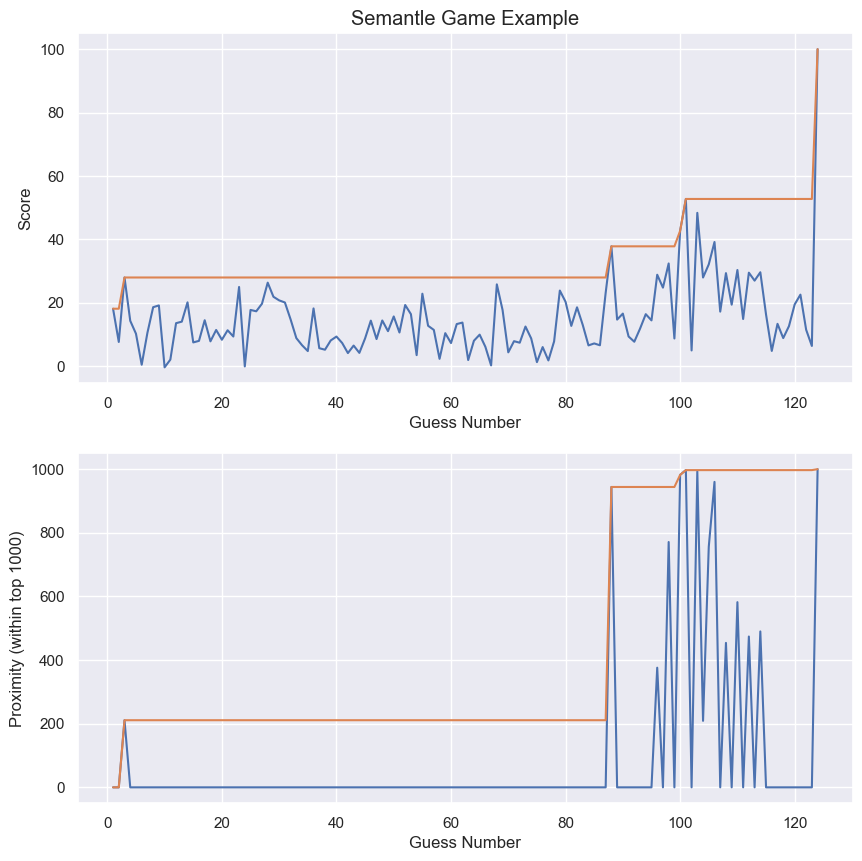
For reference, here’s a graph of the scores we might achieve, along with our proximities (defined when our guess is within the top 1000, where the upper bound is 1000) at the time. Note that towards the end, we may often guess within the top 1000, but our score still bounces around. We can also see that a game might take over a hundred guesses in total!

Blue line is the guess’s value. Orange line is the maximum value thus far.

word2vec

Naturally, we might be curious how the similarity score is computed — where does this magical number come from? Semantle actually tells us exactly how!

Semantle uses a technology called word2vec to calculate the semantic distance between words. This allows us to determine how close your guess is to the secret word. The closer you get, the more accurate the proximity column will be.

Word2vec is short-hand for “word-to-vector”, and it’s an early version of word embeddings; today’s large language models heavily depend on word embeddings (or often document embeddings) to represent semantic information!

The essential idea is that each word can be represented in a high-dimensional space as a point or vector — in Semantle’s case, we work in a 300-dimensional space. Two words that we use in similar circumstances (which often means they share similar meaning) correspond to points close to each other. The similarity score between two words measures their vectors’ cosine similarity i.e. we take the cosine of the angle between those vectors. In the game, the cosine similarity is then multiplied by 100 and rounded to the nearest hundredth to obtain the similarity score.

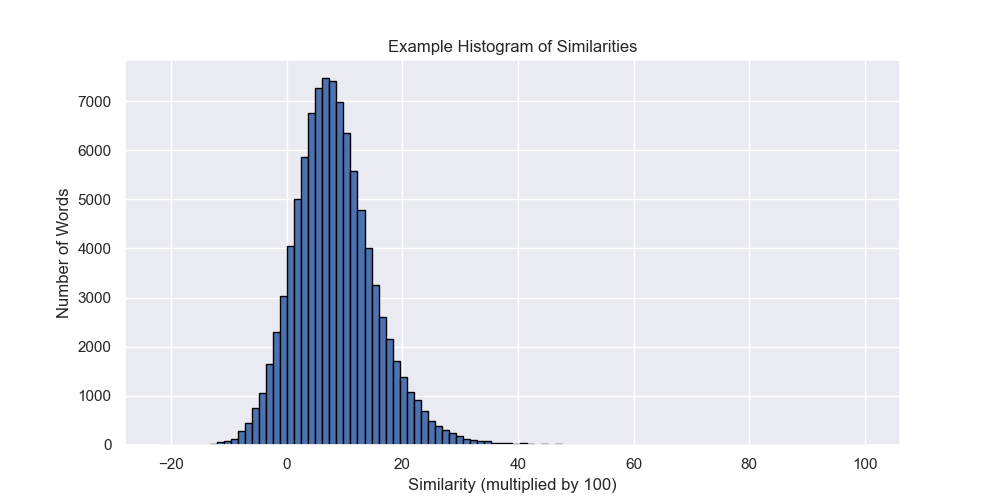
Imagine this, but in a higher dimensional space! The green right-side-up triangle represents the target word (which is “target” here), and the red upside-down triangle represents the first guess (which is “guess” here). We also label a few other words for demonstration.

In practice, most pairs of words have fairly low similarities, under 15; here’s an example of all the similarities between the word “thing” and all other words.

The vectors themselves are parameters in a neural network, trained to predict a target word based on its surrounding context words. According to this post, Google’s word2vec is trained with a continuous bag-of-words (CBOW) architecture. Such a trained model will have two sets of parameters:

(Center) word embeddings, which appear to be what Semantle uses^[2]

$$ U = \begin{bmatrix}\mathbf{u}_1 \cdots \mathbf{u}_{n}\end{bmatrix} $$

Context embeddings

$$ V = \begin{bmatrix}\mathbf{v}_1 \cdots \mathbf{v}_{n}\end{bmatrix} $$

If we want to predict a word based on nearby context words ${w_1, \ldots, w_C}$, then the prediction is based on:

$$ \begin{align*} \mathbf{h} &= \frac{1}{C} \sum_{i=1}^C \mathbf{v}_{w_i} \\ \mathbf{y} &= U^{T} \mathbf{h} \\ P(w\,|\,\text{context}) &= \frac{e^{y_{w}}}{\sum_{j=1}^n e^{y_{j}}} \end{align*} $$

Pictorially: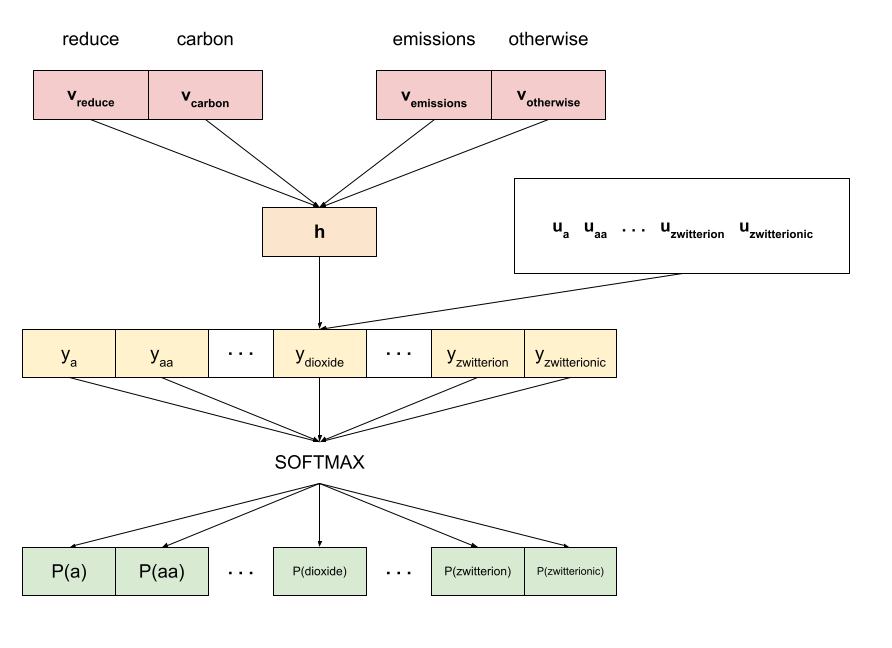

In training, the model minimizes overall cross-entropy loss, which is the negative log sum of the above probabilities across all words in the training data.

$$ \mathcal{L} = -\sum_w \log P(w\,|\,\text{context}) $$

Intuitively, this means words that often appear in the same context should have embedding vectors near each other (so that the $y_w$ term is large).

Solving in Three Guesses

Now that we’ve investigated the mechanics, let’s propose a strategy! Let’s assume that Semantle does the following:

The target is drawn uniformly^[3] randomly from the single English words in the word2vec dataset.
Whenever the game says that the guess is the nth closest word to the target, the game only considers single English words. That means even if “taylor swift” is the closest term in the embedding space (and could be guessed!), it’s not considered in the top 1000 words (here’s an example of a list). This assumption will be useful in the “Solving in One Guess?” section!

If we have the exact word2vec vectors that Semantle is using, then we should be able to narrow all but a few words after each guess. That’s because each guess tells us the target’s cosine similarity — but rounded, so there’s still a small region that the target could possibly lie in. In fact, each guess constrains the feasible region to a conical shell (or its equivalent in high dimensional space); if the guess’s vector is $\mathbf{w}_i$ and we receive a score of $z_i$, then that feasible region is: $$ R_i = \left\{ \mathbf{w} \,\middle|\, \cos (angle(\mathbf{w}, \mathbf{w_i})) \in [0.01z_i - 0.0001, 0.01z_i + 0.0001] \right\} $$ In other words, the angle between the target’s vector and the guess’s vector needs to be in a narrow band. Here’s an idea of what that region might look like if we were in a 2-dimensional embedding space rather than a 300-dimensional embedding space.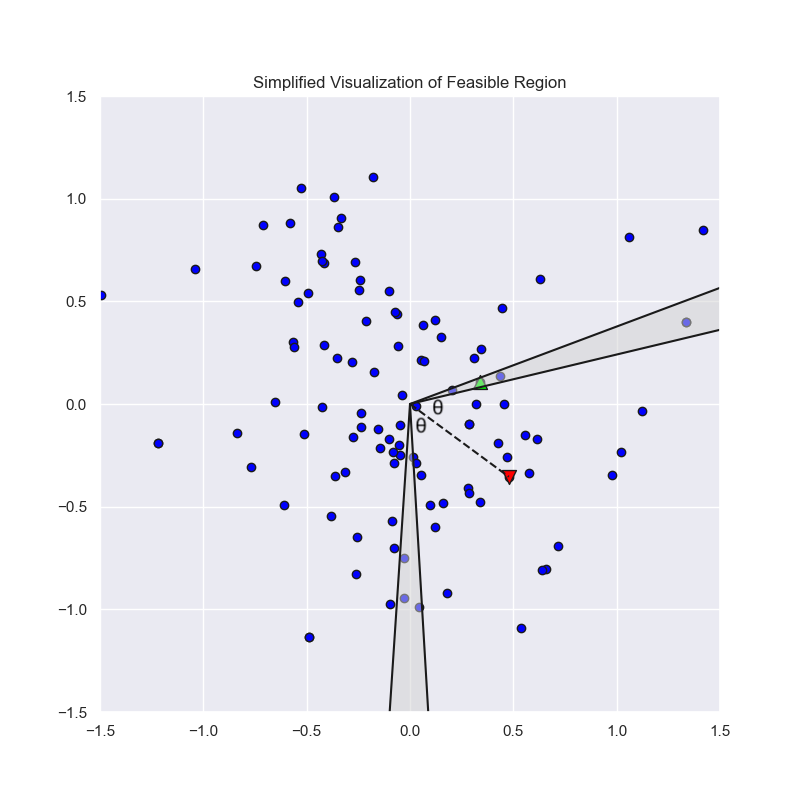

2D version of the feasible region dictated by the first guess, whose embedding vector is the red upside-down triangle. The target’s vector is the green right-side-up triangle. Now imagine this in a higher dimensional space!

As we keep guessing, our feasible region shrinks quickly: $$ R = R_1 \cap R_2 \cap \cdots $$

How many guesses does it take for the feasible region contains one vector? In practice, we can often narrow to one word in just two tries (so three guesses in total to win the game) — and it often doesn’t matter what the starting guesses are!

It also turns out that there’s a strategy to guarantee a win in three guesses.

The first guess is “tabula”. The feasible region contains about 22.5 words in expectation, the smallest among all possible first guesses.
Depending on the similarity we get^[4]:
- If the similarity is in List 1, the second guess is “rasa”
- If the similarity is instead in List 2, the second guess is “abstainer”
- Otherwise, the second guess is “uniaxial”
In each of the three cases, we’ve narrowed the region to a single word, and we guess that resulting word.

The strategy is implemented in this repository.

Solving in One Guess?

If we only depend on our guesses and the resulting similarity information, then we cannot guarantee a win in two guesses; the feasible region contains more than one candidate no matter what first guess we use. However, there’s a bit of information that Semantle provides before we even start guessing: the (rounded) similarities of the target with its nearest, 10th nearest, and 1000th nearest neighbors.

We might wonder if this information lets us solve Semantle in fewer than three guesses — maybe even with a single guess! Since we only have about 97k possible target words, we can precompute these three similarities for each one, and we can check if these similarities are unique.

Relying on just the nearest word’s similarity generally does not narrow to a single candidate
Relying on just the nearest and 10th nearest similarities gets us to a single candidate about 98.4% of the time
Relying on all three similarities gets us to a single candidate 99.998% of the time — there are exactly TWO target words that cannot be disambiguated with the rounded similarities alone!

       word  nearest_dist_rounded  tenth_dist_rounded  thousandth_dist_rounded
------------------------------------------------------------------------------
   compiler                0.7784              0.5386                   0.2658
 riverfront                0.7784              0.5386                   0.2658

That means we’re extremely likely to win with a single guess — but we’re never guaranteed to do so!

Closing Thoughts

Our analysis shows that with perfect information about the word embeddings, we can always win Semantle in 2-3 guesses. However, we humans don’t have this grasp of language; we just have heuristics around how related words are, so the above strategies aren’t applicable. To better represent these heuristics, we might pose different models:

What’s an optimal strategy if we had access to thesaurus-like information? For instance, for every word, we knew the top 20 neighbors, but without numerical similarity information?
What if we only had word2vec information for commonly used words? (It’s likely that Semantle pulls its target words from such a subset.)
What if our known similarity information was corrupted with noise?